Множество Мандельброта — это фрактал (рис. 3), определённый как множество точек на комплексной плоскости, для которых итеративная последовательность не уходит в бесконечность; Zi и C - комплексные переменные.
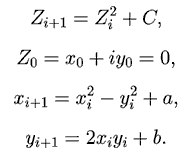
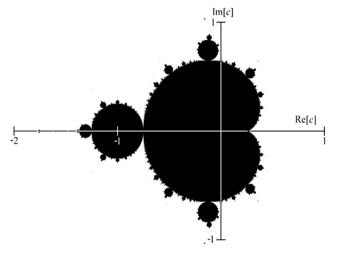
Рис. 3. Множество Мандельброта - алгебраический фрактал

Рис. 4. Шаги генерации цветного фрактала Мандельброта (32 итерации)
Берется точка комплексной плоскости с координатами (a,b), соответствующая комплексному числу c=a+bi. К этой точке n раз применяется преобразование. Если в результате n преобразований точка удалится на 2 или более единицы от начала координат, то она не принадлежит множеству Мандельброта, она окрашивается в белый цвет.
Если же расстояние от этой точки до начала координат при любом числе итераций n (допустим n=200) останется меньше 2, то точка принадлежит множеству Мандельброта и она окрашивается в черный цвет.
Для получения цветного изображения фрактала, точки, принадлежащие множеству Мандельброта, окрашиваются в цвет, зависящий от числа итераций (рис. 4).
Так как генерация фрактала – процесс итерационный, то помимо фрактальной математики требуется компьютер, а лучше, суперкомпьютер, и соответствующее программное обеспечение (рис. 5).
Программ для генерации фракталов большое множество. Большинство из них в открытом доступе (бесплатные), их легко можно скачать в интернете.
Рис. 5. Интерфейсы программного обеспечения для генерации фракталов:
а,б – Apophysys, в – Ultra Fractal, г – Mandelbulb3D
Программисты продолжают совершенствовать программное обеспечение для генерации фракталов [7-11], но следует отметить, что оно всего лишь инструмент, играть на котором приходится человеку, назовем его фрактальным дизайнером.
В этой области математическо-компьютерного дизайна требуется не карандаш, кисть и бумага, а компьютер, знание фрактальной математики и программного обеспечения, и, безусловно, так необходимый каждому художнику и дизайнеру талант.